




Jillian's Guide to Black Holes: Forming - Types - Outside - Inside - Finding - References - Websites
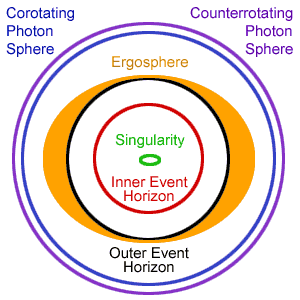
Crossection of a rotating black hole
Exactly what is rotating, here?
Why is it called a rotating black hole? The event horizon doesn't rotate --- it's just a boundary-line. I suppose it's more descriptive (and unfortunately more confusing) to say that the angular momentum of the star that made the black hole is conserved. Most stars rotate. If they become black holes that spinning motion is still there, except it is not spinning in the physical sense that the Earth spins in 24 hours. It is more like an imprint on the space around the black hole, like a memory of when it could spin for real. As a star becomes a black hole, it shrinks --- and as a rotating object gets smaller, it rotates faster. Realistically, many black holes should rotate very quickly. According to the calculations done by Kip Thorne, most black holes would rotate with a speed that is 99.8% their mass.6
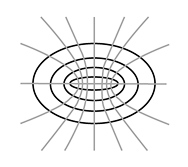
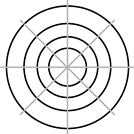
Rotating black holes are also known as Kerr black holes. It's also called a Kerr black hole for the same reason charged black holes are called Reissner-Nordstrøm black holes: Reissner-Nordstrøm geometry describes the charged black hole. The Kerr solution for the metric for spacetime describes the geometry of the rotating black hole. Since the static and charged black holes are spherically symmetric, the Schwarschild and Reissner-Nordstrøm geometries are ideally suited to polar coordinates in two dimensions and spherical coordinates in three dimensions. What're those? Well, instead of a grid of lines, things are described by a length and some angles. For the polar coords (shown left), lines of constant distance are circles; for the spherical coords, lines of constant distance are spheres. Lines of constant angle are radial lines for both systems. Kerr geometry uses something called oblate spheroidal coordinate system. It's similar to polar coordinates, except lines of constant distance are ellipses, and lines of constant angle are hyperbolae (shown right). Now, take that two dimensional grid-type-graph and rotate it about the vertical axis --- that's oblate spheroidal!
Perhaps it would be better if I just explained how a rotating black hole is different from the others. First stop ...
Two photon spheres?
What's with the doubling?! Charged black holes have two event horizons instead of one, and now rotating black holes have not only two event horizons but two photon spheres. It has to do with the fact that the black hole rotates, and, when it rotates, it "drags" the space around it into rotating with it. It's like jumping into a whirlpool. If you jump in the direction of the current and start swimming, you get propelled along and go much faster than your normal speed. If you jump in and swim against the current, you get dragged back and go much slower than your normal speed. It is the same principle for photons as they try to orbit. Instead of just having one radius where photon can orbit unstably like the other two black holes, a rotating black hole has two radii where photons can orbit: one in the direction of rotating and one against.
So there are two photon spheres. How do you tell which one goes where? Well, orbiting against the rotation of the black hole is more difficult. It's easier for me to use the example of satellites around the earth. Take two satellites, one further from the earth and one closer to the earth. The one closer to the earth must go much faster in order to stay in orbit and not go crashing down to the planet below. The satellite further away can go slower and still stay in orbit. O-K. Now, back to the black hole. Say you've got two light rays, one going in the direction of rotation and one going against it. You can draw a rough parallel between the two situations (a not-entirely-scientific parallel because the speed of light is a constant). The light ray going in the direction of rotation can kinda "go faster," so it can orbit closer to the black hole. The light ray going against the rotation kinda "goes slower," so it must orbit further away from the black hole.
Oh, did I say it had two photon spheres? Heehee. That's not quite accurate. See, since the black hole rotates, it's got an axis of rotation. It's no longer spherically symmetric like the other two. Its structure depends on what angle at which you approach the black hole. If you approach in the direction of the equator, then what I told you stands true: two photon spheres. If, however, you approach at an angle to the equator (you know, just like lines of latitude on the earth), there is only one photon sphere. Why? Well, if you come in from the top, there isn't really a choice of whether you should go with or against the rotation.
What's between the photon spheres?
A sensible question. Between the counterrotating and the corotating photon spheres are the different photon spheres for light rays approaching the black hole not quite on the equator. This is confusing, so perhaps I should use another example. Imagine that you're floating above the Earth in a spaceship. Let us say there are three landing strips you can use: on the equator in Equador, further from the equator at Syracuse, New York, or on the axis of rotation at the North Pole. Replace the Earth by a rotating black hole and your spaceship by a light ray. If you came in towards "Equador," you would encounter the counterrotating photon sphere at one point, and you could merrily and unstably orbit the black hole against the direction of rotation. Going in further you would find the corotating photon sphere, and you could happily orbit unstably in the direction of rotation. If you came in towards "Syracuse" or the "North Pole," there would only be one photon sphere for ya.
The placement of the two photon spheres all depends upon the speed of rotation. For a slowly rotating black hole the two are so close to one another (on the equatorial plane, remember) that it's almost like the photon sphere of a non-rotating black hole. The faster the black hole rotates, the further apart the two photon spheres are. A black hole that rotates with a speed as great as its mass (again, the numbers we're blithely bandying about are sickeningly huge, since the mass of the smallest possible black hole is 5.7 x 1030kg --- meaning it would have to have an angular velocity of 5.7 x 1030 meters per second) has the greatest distance between the two photon spheres.
Ergosphere
The ergosphere is not a photon sphere, nor is it an event horizon. It's something very special to rotating black holes. Firstly, what does it look like? It is a solid ellipsoid (a 3D ellipse) that billows out from the black hole above the outer event horizon. The faster the black hole rotates, the further it billows. This is unusual cuz it's the first thing I've mentioned that is not just a radius, it is, in fact, a region. The photon spheres and event horizons are just distances, after all; but not the ergosphere. By the by, the most the ergosphere can billow out is when its radius (along the axis of rotation) is 1/2 Rs.
The outer boundary of the ergosphere is the static limit of the rotating black hole. What's that? It's where you can no longer stay still, even if you were going at the speed of light. For static black holes the static limit is the event horizon, since after you cross that, even if you go the speed of light, you are pulled towards the singularity. A rotating black hole is different from the other two (once again!) in that its static limit is above its outer event horizon.
This is all very nice, but what does it mean?! It means that once you cross into the ergosphere, it is impossible to stay still. Even light rays are dragged along in the direction of rotation. However, you can enter and leave this region whenever you like, unlike the abandon-all-hope-ye-who-enter-here static limit/event horizon of the other two black holes. You can merrily weave in and out of the ergosphere with no nasty side-effects. It's a place of quirky spacetime of the black hole that we can actually visit and leave.
Familiar horizons
The two event horizons of the rotating black hole are pretty much the same as a charged black hole's event horizons: two radii where a distant observer would say time seems to stop. The outer horizon switches time and space around one way, and the inner horizon flips 'em back to how they are in the real world. Oh, I didn't explain that stuff when I talked about charged black holes, right? It's pretty complicated and it's easier to understand if you know how to read spacetime diagrams. I go into detail in the Inside section.
Briefly, we normally go about life moving around as we please in space but being inexorably dragged by time. Whenever you cross any event horizon, those two things ... flip. That's why I edged a lot when I mentioned the singularity. Due to this flipping, it is not a point in space; it's a time. After a certain time after you cross a static black hole's event horizon, what's left of you might survive to encounter the singularity. What about charged and rotating black holes and their two horizons? That's what make's 'em special. When you cross the second horizon, space and time flip back to what we're used to experiencing and the singularity becomes a place in space and entirely possible to avoid. Back to the topic at hand!
The rotating black hole has an outer and an inner event horizon. They each move closer to one another the more angular velocity the black hole has. When the speed of the black hole's rotation equals its mass, the two event horizons merge into one. When you cross this, you don't even bat an eyelash because there is no flipping of space and time at all. Should the black hole spin faster than that, both horizons disappear and leave the exposed singularity. Everyone calls this a naked singularity so often that I've sworn off using the term completely.
Ring around the singularity
The singularity is a ring, you see. Calculations using Kerr geometry describe the singularity as ring-shaped. That's a curious concept. It's also much more complicated than that! I go into detail about singularities in the Inside section for a reason --- I want to keep all the wackiness in one place. Still, ring singularities are just so neat that I can't contain myself.
You already know that a traveler can move about quite freely after crossing the inner event horizon. Space and time are in their usual places. What you don't know is that you actually have to make an effort to hit the singularity of a rotating black hole! If you approach it from any angle other than equatorial, you could travel the universe or to other universes. You could turn around and leave the black hole. Sure, you'll emerge way in the future of your own universe, but, considering that the nearest black hole is many, many light years away, you'll probably have expected some time dilation from your method of getting to the darned thing in the first place. Where you go if you point yourself towards to singularity depends on who you talk to. Some physicists like to call it 'negative space.' Others (myself included) like to call it another universe or another part of this universe.
You could just sit there and admire the view. The singularity would appear like an oval window. If you looked at it from the axis of rotation, it would be a circular window. The closer you got to the equator, the more oval the window would seem. At the equator, you would only see the singularity. But ... what would the oval window show you?


